理解してから進むか、丸暗記するか、どちらがいいの？

解説を読んでも何が何だかよくわからない。ただ、ここの数字とここの数字をかけて、ここの数字を足してやれば答えは出てくる。次のテストにはこの問題が出てきそうだ。とりあえずやり方を丸暗記でいいかな？

こんな経験ありませんか？

丸暗記だと応用がきかない、どこかでつまづくという意見があります。あるいは、理解してから進もうとすると、時間がいくらあっても足りない、という意見もあります。

理解してから進むか、丸暗記するか、どちらがいいのでしょうか？

速さの公式、割合の公式

速さの公式に「き（距離）＝は（速さ）×じ（時間）」という覚え方があります。

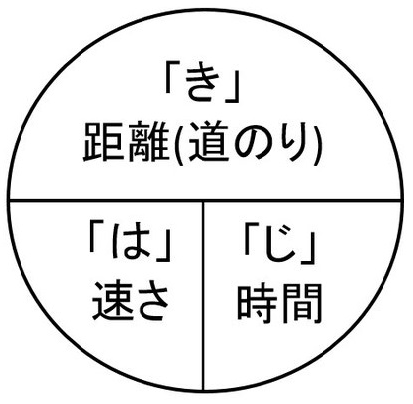
「きはじ、きはじ…」と丸暗記です。あるいは「キティちゃんの鼻血（はなぢ）」などという覚え方もあります。初回には鉄板で笑いが取れるやつです。

「木下（きのした）のハゲじいさん」という覚え方もあるそうです。何でもありですね。

さらに割合の公式に「く（比べる数）＝も（もとにする数）×わ（割合）」もあります。「くもわ、くもわ…」と丸暗記です。

ただ、この場合「比べる数」と「もとにする数」が、見分けられないという人がいます。そこで「の」は「もと」、「は」は「くらべる」と覚えます。

こういう問題のとき、「体育が好きな人は」だから「比べる数」、「クラス全体の」だから「もとにする数」と考えるのです…ここまでくると、なんのこっちゃ、という感じですね

さて、この「速さの公式」と、「割合の公式」の丸暗記はどうなのでしょうか。これはよく話題になっています。そして「なぜそうなるのかを、ちゃんと理解させないといけないのではないか」という意見が大多数です。

私も教えるとき、一応、理解させようとはします。

「こうコップがあるとするね。そのうちこれだけ水が入っている感じ。満タンが100とすると、30入っているんだね。で、コップ全体が40人だから…」

理解する子はすぐに理解します。ですが、そうでない子は、正直なかなか難しいです。その場合、上記の「丸暗記の公式」を教えることになります。

三角形の面積の公式

三角形の面積を求める公式は「底辺×高さ÷2」です。当たり前ですよね。誰でも知っています。でもこれって、どうやって出てきたのでしょうか。

この公式のもともとは、平行四辺形の面積を求める公式「底辺×高さ」を、半分にしたものです。案外忘れがちなんですよね。さらに言えば、その平行四辺形の公式も、平行四辺形を変形させると、長方形になるということから、長方形の面積の公式を流用したものです。

これを理解していると、三角形の底辺と高さがどこなのかを、間違えなくなります。とはいえ、そういうことを理解していなくても、ほぼ問題がないほど、三角形の面積を求める公式は浸透しています。

ひし形の面積を求める公式は「対角線×対角線÷2」です。これは「同じ形の三角形が2つある」と考えることで、導くことができます。でも、公式を覚えていたら一発ですね。

そんなことを言っていたら球の体積を求める公式はこうなります。「身の上に心配があるので参上する」…なぜそうなるのかなんか、どうでもいいですよね。

「ニーエーブンノマイナスビープラスマイナスルートビーニジョウマイナスヨンエーシー」…解の公式の呪文です。これもなぜそうなるのかという説明がテキストの隅に書いてありました。しかし、誰もそれを見ようともしません。

掛け算の九九、乗法公式

ふりかえってみると、掛け算の九九があります。「はちしち」とくれば「56」です。理屈は「8＋8＋8＋8＋8＋8＋8＝56」です。ですが、誰もそれを考えません。それでいいのではないでしょうか。

掛け算では、7の段を苦手としている人がいます。そんなとき冗談で、「足し算でやってみたら？」とは言います。でも本当にやりだしたら、「100回口に出して、暗記しなさい！」と言います。

掛け算の九九を丸暗記しないと、その後の計算で困るからです。九九は理屈ではなく、丸暗記しなくてはなりません。

乗法公式の問題も同様です。乗法公式の理屈はこうです。

(ｘ＋3)(ｘ－4)
＝x²＋3x－4x－12
＝x²－x－12

ですが、公式を使うと、途中式を省いてこうなります。

(ｘ＋3)(ｘ－4)
＝x²－x－12

そしてこれは、「理屈は忘れて、公式のやり方を体に叩き込みなさい」と教えます。そして分配法則を使って途中式を書いていたら、やり直しさせます。でないと、因数分解で困るからです。

理屈から離れることによって、スピードが上がります。そして理屈から離れることによって、その先に進むこともできます。むしろこれらは、理屈を捨てて丸暗記すべきです。

まとめ

公式やその問題の解き方を覚えるとき、「理解してから進むか、丸暗記するか」について書いてみました。

結論は、「丸暗記すればよい」です。ただ軽くでもいいので、理由に触れておくのがいいですね。その結果、理解できればそれでいいですし、理解できなければそれはそれでいいです。

理屈が分からなくても使っているものは、世の中に山ほどあります。普段使っているスマホもそうです。話したり、メールしたり、写真を撮ったり、ゲームをしたりしますが、その理屈なんて知りませんよね。

そして必要に迫られれば、あるいは興味がわけば、その理由に再び取り組めばよいのではないでしょうか。ある程度先に進んでから、振り返って確認するのもよいでしょう。

ぐるっと回ってから確認すると、寄り道した分、違った面から確認することができるかもしれません。そしてそのおかげで、理解しやすくなることもあります。物事の到達への道のりは1つではないのです。

最初の例の「速さ」や「割合」の話ですが、小学校の間は分からなくても、中学校に入って問題をこなしていくうちに、理解する人が出てきます。そういうものです。

今は分からなくても、後で理解できるかもしれません。それを期待して、とりあえず丸暗記でやっておけばいいんじゃないでしょうか。